Separating Reflections From a Single Image Using Local Features Posted on May 15, 2007 by Dave Fowler
I said a while ago that I'd get around to slowly posting a few of the things I've been working on. A week ago I presented my final project for Image Processing along with my partner Jonathan Waltz. It was to implement Separating reflections from a single image using local features, a paper by A. Levin, A. Zomet and Y. Weiss. For the presentation details check out our slides here.
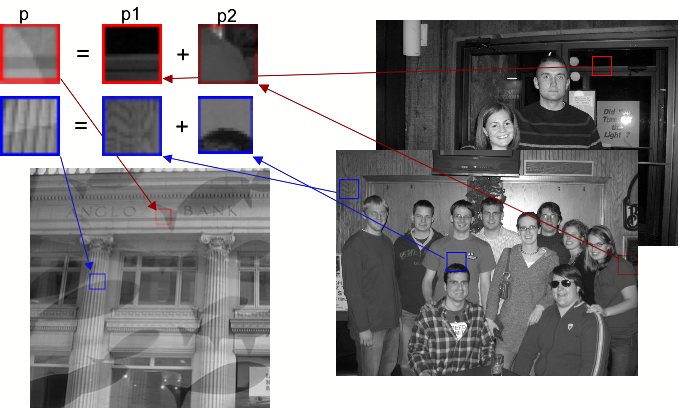
The goal of the paper is to take a single image with reflections and separate it into two images without reflections. The advantage? When you take a picture from your car, tour bus or through the window at your office you can now remove the extra crap you get from the window reflections! Sounds easy enough but its actually an incredibly difficult and computationally expensive task. The problem can be represented by the equation
where I is the original image and I1 and I2 are the desired separated images. The image of the overlapping box and circle depict the equation. Practically speaking there are an infinite number of different I1's and I2's that sum up to the original image! Though its visually easy for us to pick apart the two images, a box and a circle, a computer has a much tougher time.
But we can't let the large task keep us from trying. Large tasks are what computers are made for right!? Instead we break the image down into overlapping 7x7 pixel patches. Then we use the benefits of a natural image database! I learned a lot about these things but its still crazy to me how they work. Basically a database of a bunch of "natural" or common images are used to gain further information on what our two images should look like. I built our database by collecting all 7x7 patches in two photographs I stole from my friends on facebook. Then with the use of derivative and directional filters the approximately 100k samples are compared to the derivatives of the original image patches.
The goal is to solve the original problem equation for each patch, p = p1 + p2. Advantaging the scarcity of the derivative we find a p1 that's closest to p, and then a p2 that best fits p2 = p - p1. One set of p1's and p2's isn't enough. Instead the best 10 sets are used, and scrambled into 40 different p1 and p2 combinations. Finding the combinations is a very computationally expensive task, as for each of the original patches 11 patch compares must be done on each of the 100k samples in the database. Note: don't do this in Matlab, it takes forever. I'd done all the other Image Processing assignments in Matlab just because it was familiar after taking Computer Vision last spring. I quickly realized that I'd have to find a C++ API. I tried several out but I either had porting issues with my mac or found it to be way too much overhead with an annoying learning curve. All I wanted was a simple program to read an image file into an array I could manipulate in C. After a few impatient hours of trying other API's I ended up finding some sample code by Guillaume Cottenceau based on the png library and built my own. Its just a simple Image class that handles reading and writing the image and contains the 2D array of the data. It also has a convolution tool and the default example shows how to do a Sobel filter on an image. Just download it here and run the following commands.
$ make
$ ./Sample danandmegan.png
$ open sobel.png
I'll write more on it later.
Anyway, I built that simple API and then a bunch of tools for building and matching with the natural image database. The matches are then compared to the surrounding probable patches using a technique called loopy belief propagation. That's the part I sucked at and still don't get. I was pretty upset about the fact that I had gotten so far, written so much code and wasn't able to finish. This is the first project that, though I worked pretty hard at it and did some awesome stuff I still wasn't able to complete by the deadline. I gave myself far too little time, dramatically underestimated the project which was more like 3 paper implementations than one, and had several time consuming hold ups. Eighteen years of school and I'm only now learning my lesson :). I still got a decent grade and may come back to finish it sometime in the unprobable future where I have loads of free time.
Dave